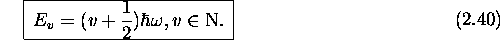
On trouve que (2.39) ne possède de solutions normables qu'à des valeurs de l'énergie quantifiée selon la loi simple suivante (voir problème 8)
Les niveaux d'énergie de l'oscillateur sont donc équidistants, et
le premier niveau se situe à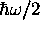 
du fond du potentiel. Ce niveau
fondamental est appelé le niveau zéro de l'oscillateur. Chaque
niveau 
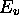est non-dégénéré et la fonction propre associée est de la
forme
où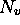 
est une constante de normalisation et 
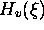est un
pôlynôme, appelé pôlynôme d'Hermite, de la variable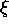 
. Le tableau
2.1 donne l'expression explicite des premiers
pôlynômes d'Hermite.
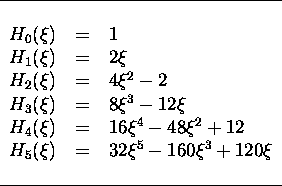
Table 2.1: Expression des premiers pôlynômes d'Hermite.
La figure 2.6 montre le graphique des premières
fonctions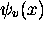 
ainsi que celui de leurs densités de probabilité de
présence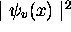 
. On note les mêmes structures nodales que
celles des fonctions propres d'une particule dans une boîte
uni-dimensionnelle. Dans la limite des très grandes valeurs de v, la
distribution de probabilité se rapproche de plus en plus de celle
prédite par la mécanique classique, dans laquelle, l'oscillateur
réside pour la majeure partie du temps au voisinage des points de
rebroussement définis par l'intersection du potentiel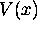 
avec le
niveau E. Cette tendance est illustrée à la figure 2.7.
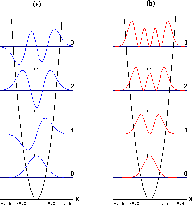
Figure 2.6: Les premiers niveaux d'énergie de l'oscillateur
unidimensionel avec (a) leur fonction
propre associée, (b) la distribution de probabilité de
présence associée.
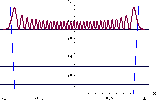
Figure 2.7: Distribution de probabilité de présence associée
à v = 30 d'un oscillateur harmonique unidimensionel
Le moment dipolaire d'une molécule diatomique dans son état électronique fondamental est généralement une fonction analytique de la distance internucléaire R. On peut donc la développer, en série de Taylor, sous la forme
où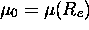 
et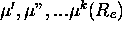 
sont les première, seconde et généralement k-ième dérivées de l'amplitude de 
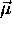par rapport à R, toutes évaluées en 
.
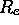Si toutes ces dérivées sont nulles, c'est à dire que le moment dipolaire permanent est une constante par rapport à R, alors
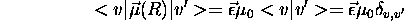
et aucune transition vibrationnelle ne serait possible, car, selon eq.(1.39) du chapitre 1,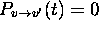 
dans ce cas, et ce pour toute paire 
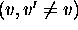. On ne peut donc avoir une spectroscopie vibrationnelle que si la molécule diatomique possède un moment dipolaire permanent qui varie de façon non-triviale au cours des vibrations.
Très souvent, la série (2.42) est dominée par le terme linéaire en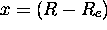 
et le moment de transition gouvernant le spectre vibrationnel pur se réduit à
(voir problème 8 pour la démonstration de ce résultat), d'où la règle de sélection:
bien connue en spectroscopie vibrationnelle.
