



Next: Exercices
Up: Oscillateur harmonique
Previous: Oscillateur unidimensionnel: Solutions
Pour un oscillateur multidimensionnel, décrit par (2.38) et
modélisant les n modes normaux d'une molécule polyatomique, on
obtient, après la séparation de variables mentionnée
précédemment
- Quantification de l'énergie
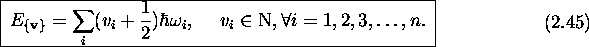
- Fonction propre
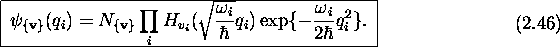
- Règles de sélection:
Il suffit de remplacer le développement de eq.(2.42) par
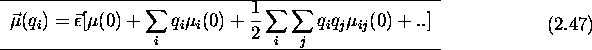
où 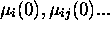 sont des dérivées de
sont des dérivées de 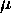 par rapport à
par rapport à 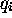 ,
, 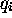 et
et 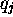 , toutes évaluées à la géométrie d'équilibre de la molécule. Eq.(2.48) se généralise en
, toutes évaluées à la géométrie d'équilibre de la molécule. Eq.(2.48) se généralise en
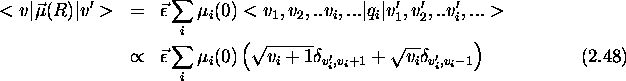
et les règles de sélection pour le cas de n modes sont

À titre d'exemple, considérons la molécule 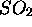 dans l'approximation harmonique. Les trois
modes normaux de cette molécule sont
dans l'approximation harmonique. Les trois
modes normaux de cette molécule sont
- mode de valence symmétrique,
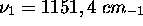 ,
,
- mode de déformation,
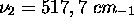 ,
,
- mode de valence asymmétrique,
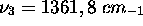 .
.
Le tableau 2.2 compare les prédictions théoriques du
spectre vibrationnel de cette molécule avec les observations
expérimentales. On note que l'approximation harmonique donne une image
fort fidèle des vibrations de cette molécule. On note aussi que les intensités des bandes du spectre confirment la règle de sélection (2.49), c.à d. la dominance du terme linéaire dans le développement de 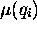 .
.
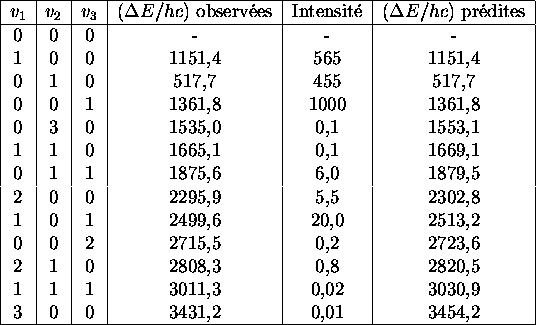
Table: Transitions observées dans le spectre vibrationnel de
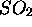 , comparées
aux prédictions théoriques basées sur l'approximation harmonique.
Les intensités des transitions sont relatives à la transition
, comparées
aux prédictions théoriques basées sur l'approximation harmonique.
Les intensités des transitions sont relatives à la transition
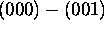 , qui est normalisée arbitrairement à 1000
, qui est normalisée arbitrairement à 1000
Cours WWW Intro a la Chimie Quantique
Sat Jan 13 22:02:54 EST 2001
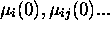 sont des dérivées de
sont des dérivées de 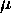 par rapport à
par rapport à 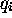 ,
, 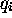 et
et 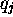 , toutes évaluées à la géométrie d'équilibre de la molécule. Eq.(2.48) se généralise en
, toutes évaluées à la géométrie d'équilibre de la molécule. Eq.(2.48) se généralise en
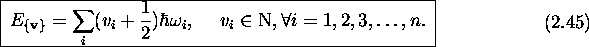
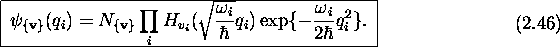
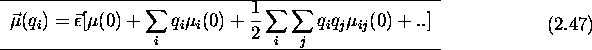
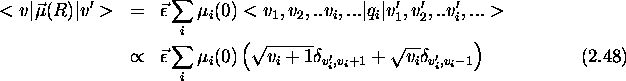

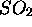 dans l'approximation harmonique. Les trois
modes normaux de cette molécule sont
dans l'approximation harmonique. Les trois
modes normaux de cette molécule sont
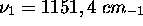 ,
,
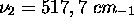 ,
,
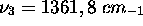 .
.
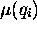 .
.

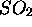 , comparées
aux prédictions théoriques basées sur l'approximation harmonique.
Les intensités des transitions sont relatives à la transition
, comparées
aux prédictions théoriques basées sur l'approximation harmonique.
Les intensités des transitions sont relatives à la transition
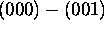 , qui est normalisée arbitrairement à 1000
, qui est normalisée arbitrairement à 1000