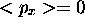 dans tout état stationnaire de la
particule dans une boite unidimensionnelle.
dans tout état stationnaire de la
particule dans une boite unidimensionnelle.

est une fonction propre de l'opérateur 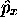 . Quelle en est
la valeur propre? Vérifiez que cette fonction propre est bien normée
sur la boite
. Quelle en est
la valeur propre? Vérifiez que cette fonction propre est bien normée
sur la boite 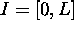 .
.
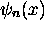 , (2.10) sous la forme
, (2.10) sous la forme
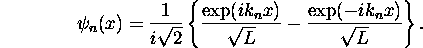
En utilisant les résultats de l'exercice précédent, déterminez
la probabilité que l'impulsion, 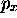 , de la particule
préparée dans l'état
, de la particule
préparée dans l'état 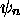 vaut i)
vaut i) 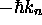 , ii)
, ii)
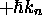 , iii) une valeur quelconque autre que
, iii) une valeur quelconque autre que 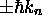 .
.
Pouvez-vous expliquer le résultat 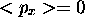 sur la base de
vos observations?
sur la base de
vos observations?
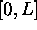 . On supposera que cette particule est préparée au temps t=0 dans l'état normé suivant:
. On supposera que cette particule est préparée au temps t=0 dans l'état normé suivant:
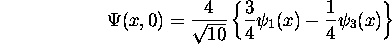
où
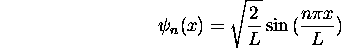
est la fonction propre normée de 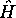 associée à la valeur propre
associée à la valeur propre 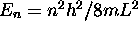 .
.
- En déduire l'expression de la fonction d'état
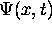 à un temps t>0.
à un temps t>0.
- Déterminez la probabilité de trouver, au temps t, la particule possédant
-
une énergie
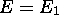 ,
,
- une énergie
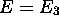 ,
,
- une impulsion
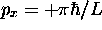 ,
,
- une impulsion
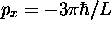
-
une énergie
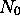 molécules considérées comme des particules indépendantes, se mouvant librement dans une boîte cubique de côté L.
molécules considérées comme des particules indépendantes, se mouvant librement dans une boîte cubique de côté L.
- Construisez un diagramme de niveaux d'énergie pour ce système, montrant tous les niveaux d'énergie inférieure à
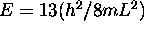 . Indiquez la dégénérescence respective de chaque niveau.
. Indiquez la dégénérescence respective de chaque niveau.
La boîte bidimensionnelle carrée peut-être utilisée dans un modèle simple de la chlorophylle, un système de 26 électrons
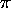 conjugués dans un plan.
conjugués dans un plan.
- Écrivez l'hamiltonien décrivant ce système en traitant les 26 électrons
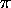 comme des particules indépendantes se mouvant dans la boîte.
comme des particules indépendantes se mouvant dans la boîte.
- Esquissez toutes les séparations de variables que l'on doit effectuer pour décrire les états stationaires de la chlorophylle dans ce modèle.
Oscillateur harmonique
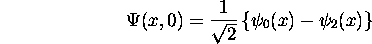
où
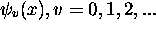 sont des fonctions propres normées de l'hamiltonien
sont des fonctions propres normées de l'hamiltonien 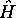 de l'équation (2.37).
de l'équation (2.37).
- En déduire l'état vibrationnel de la molécule
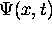 à un temps t>0.
à un temps t>0.
- Déterminez la probabilité que la molécule ainsi préparée possède, au temps t
-
une énergie vibrationnelle de
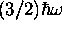 ,
,
- une énergie vibrationnelle de
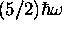 .
.
-
une énergie vibrationnelle de
- Calculez la valeur moyenne de l'énergie vibrationnelle de la molécule à un temps t>0.
- Vérifiez que

est la fonction propre de
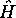 associée à l'état fondamental de l'oscillateur.
associée à l'état fondamental de l'oscillateur.
- Définissant
avec
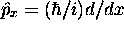 , montrez que
, montrez que 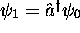 est une fonction propre de
est une fonction propre de 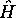 avec valeur propre
avec valeur propre 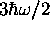 .
.
L'opérateur
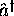 et son conjugué hermitique (adjoint),
et son conjugué hermitique (adjoint),
jouent un rôle central dans la théorie quantique des vibrations harmoniques. Ils sont appellés opérateurs de création et d'annihilation respectivement à cause des relations suivantes
qui décrivent l'action de ces opérateurs sur les fonctions propres normées
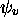 de
de 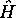 .
.
- Démontrez la relation de commutation suivante:
- Démontrez la relation suivante:
- Vérifiez que
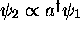 (
(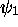 a été définie ci haut) est fonction propre de
a été définie ci haut) est fonction propre de 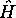 avec valeur propre
avec valeur propre 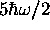 .
.
- En employant les propriétés qu'on vient de citer des opérateurs
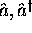 , (2.53), (2.54) et (2.55) incluant leur définition, (2.52) et (2.51), démontrez, pour tout état stationaire
, (2.53), (2.54) et (2.55) incluant leur définition, (2.52) et (2.51), démontrez, pour tout état stationaire 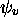 de l'oscillateur harmonique, les résultats suivants:
de l'oscillateur harmonique, les résultats suivants:
- <x> = 0,
-
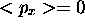 ,
,
-
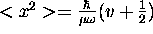 ,
,
-
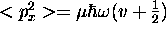 ,
,
-
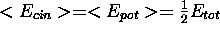
- Démontrez la relation suivante (règle de sélection):
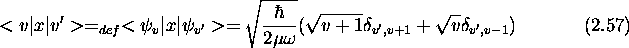
où 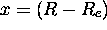 et
et 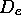 est l'énergie de dissociation de la molécule. Développez la fonction
est l'énergie de dissociation de la molécule. Développez la fonction 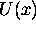 en série de Taylor au voisinage de x=0 pour obtenir, au second ordre, un potentiel décrivant un oscillateur harmonique. Comment la constante de force, donc la fréquence de l'oscillateur sont-elles reliées aux paramètres
en série de Taylor au voisinage de x=0 pour obtenir, au second ordre, un potentiel décrivant un oscillateur harmonique. Comment la constante de force, donc la fréquence de l'oscillateur sont-elles reliées aux paramètres 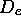 et
et 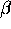 de (2.58)?
de (2.58)?
Pour HCl, 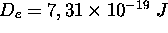 et
et 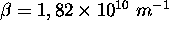 . Calculez la constante de force de rappel de HCl.
. Calculez la constante de force de rappel de HCl.
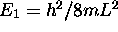 , l'énergie de l'état fondamental et celle du premier état excité du système? Donnez la dégénérescence respective de chacun de ces niveaux.
, l'énergie de l'état fondamental et celle du premier état excité du système? Donnez la dégénérescence respective de chacun de ces niveaux.





