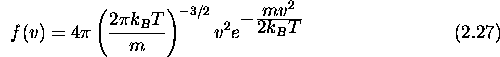d'une particule de masse
d'une particule de masse 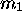 d'un corps massif, de masse
d'un corps massif, de masse 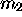 , comme la terre, est définie par la condition
, comme la terre, est définie par la condition
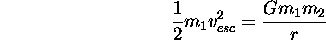
où r est la distance séparant le centre des 2 corps initialement, et 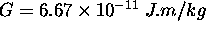 est la constante gravitationnelle.
est la constante gravitationnelle.
- Déterminez la vitesse d'échappement d'une molécule
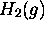 et celle d'une molécule
et celle d'une molécule  de la terre (
de la terre (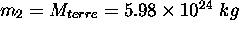 , le rayon terrestre est
, le rayon terrestre est 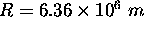 ).
).
- À quelle température ces molécules de gaz devraient-elles se trouver pour être animées d'une vitesse (radiale) moyenne égale à leur vitesse d'échappement?
- Répétez les calculs précédents pour la vitesse d'échappement des mêmes molécules de la surface lunaire. La masse de la lune est
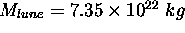 , son rayon,
, son rayon, 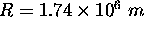 .
.
 . Chaque disque porte une fente radiale et les disques sont disposés de telle sorte que les fentes associées à 2 disques consécutifs sont décalées d'un angle
. Chaque disque porte une fente radiale et les disques sont disposés de telle sorte que les fentes associées à 2 disques consécutifs sont décalées d'un angle  fixe. On trouverait une illustration de ce dispositifs à la figure 1.14 de Atkins, figures 27.8, 27.9 de McQuarrie et Simon, et une simulation animée au site web suivant:
fixe. On trouverait une illustration de ce dispositifs à la figure 1.14 de Atkins, figures 27.8, 27.9 de McQuarrie et Simon, et une simulation animée au site web suivant:
http://www.carlton.paschools.pa.sk.ca/chemical/KineticEnergy/TempAndKE.htm
- Montrez qu'à une valeur fixée de
 , le dispositif ne laissera passer que des molécules de vitesse
, le dispositif ne laissera passer que des molécules de vitesse

- Soit
 ,
, 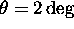 . Déterminez la gamme de vitesses des molécules sélectionnées que l'on peut couvrir en variant
. Déterminez la gamme de vitesses des molécules sélectionnées que l'on peut couvrir en variant  de 0 à
de 0 à 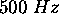
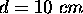 avec des fentes décalées de
avec des fentes décalées de  d'un disque à l'autre, entre une source (four) d'atomes Kr et un détecteur de tels atomes.
d'un disque à l'autre, entre une source (four) d'atomes Kr et un détecteur de tels atomes.
En faisant varier la fréquence de rotation,  , des disques, on a obtenu les résultats suivants, où
, des disques, on a obtenu les résultats suivants, où 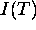 est l'intensité du faisceau de Kr détecté à la température T:
est l'intensité du faisceau de Kr détecté à la température T:

En portant  en fonction de
en fonction de 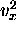 , où
, où  est la vitesse de translation (1D) des atomes détectés à une fréquence de rotation
est la vitesse de translation (1D) des atomes détectés à une fréquence de rotation  , montrez que la distribution de vitesse expérimentale est bien conforme à la loi de Maxwell-Boltzmann.
, montrez que la distribution de vitesse expérimentale est bien conforme à la loi de Maxwell-Boltzmann.
Considérons maintenant un 'gaz 2D', où les molécules sont confinées à se mouvoir dans un plan.
Comment doit-on modifier eq.(2.27) pour décrire la distribution 'radiale' dans ce cas? Obtenez, pour ce cas 2D, l'expression explicite de la vitesse radiale moyenne <v> en fonction de la température T et de la masse moléculaire m.
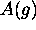 est défini comme étant la distance moyenne parcourue par cette molécule entre deux collisions. Le temps séparant deux collisions étant
est défini comme étant la distance moyenne parcourue par cette molécule entre deux collisions. Le temps séparant deux collisions étant

où 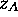 est la fréquence de collisions subies par la molécule considérée, c.à d.
est la fréquence de collisions subies par la molécule considérée, c.à d.

On peut alors définir le libre parcours moyen par
où <v> est la vitesse (radiale) moyenne des molécules de gaz.
Montrez que l'on peut écrire  en termes de la température T, la pression P du gaz et la section efficace de collisions
en termes de la température T, la pression P du gaz et la section efficace de collisions 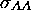 de la façon suivante:
de la façon suivante:
- Calculez, à
 , le rapport de (a) la vitesse moyenne, (b) l'énergie cinétique moyenne de molécules
, le rapport de (a) la vitesse moyenne, (b) l'énergie cinétique moyenne de molécules 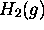 et d'atomes
et d'atomes  .
.
- Calculez le libre parcours moyen d'une molécule
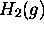 et celui d'un atome
et celui d'un atome  à
à 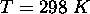 et
et 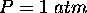 . On donne
. On donne  et
et 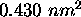 pour
pour  et
et 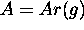 , respectivement.
, respectivement.
- À quelle pression le libre parcours moyen d'un atome
 , à
, à  , serait-il égal à la dimension d'un volume (cubique) de un litre?
, serait-il égal à la dimension d'un volume (cubique) de un litre?
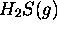 considérée (a) un gaz parfait, (b) un gaz de Van der Waals avec
considérée (a) un gaz parfait, (b) un gaz de Van der Waals avec  dans des conditions de volume et de température suivantes:
dans des conditions de volume et de température suivantes:
-
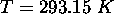 ,
, 
-
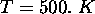 ,
, 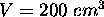
-
Un gaz à
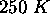 et
et 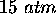 a un volume molaire
a un volume molaire  plus petit que celui calculé par la loi des gaz parfaits. Calculez ce volume et indiquez laquelle des deux types de forces intermoléculaires, (force attractive ou force répulsive), est dominant au sein de ce gaz.
plus petit que celui calculé par la loi des gaz parfaits. Calculez ce volume et indiquez laquelle des deux types de forces intermoléculaires, (force attractive ou force répulsive), est dominant au sein de ce gaz.
- même question pour un gaz dont le volume molaire à
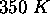 et
et 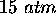 est
est 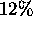 plus grand que celui prédit par la loi des gaz parfaits.
plus grand que celui prédit par la loi des gaz parfaits.
 . Son volume molaire à
. Son volume molaire à 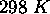 et
et 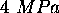 se trouve égal à
se trouve égal à  .
.
- Quelle est la valeur de la constante b de Van der Waals pour ce gaz?
- Déterminez le point critique de ce gaz.