On peut montrer que les résultats précédents, dont le
caractère ``différentielle exacte'' de 
surtout,
s'appliquent aussi bien à un système arbitraire B, en
considérant ce système en contact thermique avec un gaz parfait
(appelons le A) formant un supersystème A+B isolé. Alors la
première loi implique que pour tout processus réversible dans A (qui
est nécessairement accompagné par un processus réversible
correspondant dans B), on a
Pour un processus réversible cyclique, on a donc
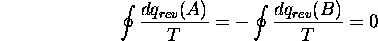
en vertu de eq.(4.3). La quantité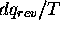 
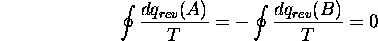
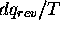est donc une différentielle exacte, que l'on peut encore une fois identifier
à la variation infinitésimal, la différentielle, d'une fonction
d'état, l'entropie S.