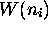La définition de l'entropie en mécanique statistique utilise la
fonction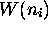 
, le nombre de complexions, ou la
dégénérescence de l'état macroscopique, défini au
Chapitre 1, eq.(1.12). Elle se lit simplement
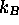étant la constante de Planck. Rappelons que
de sorte que
La définition statistique de S peut donc se lire encore
où 
est la probabilité de trouver une molécule sur le
niveau 
, qui est donnée par la loi de Maxwell-Boltzmann,
eq.(1.17) du Chapitre 1. Il est utile de la
rappeler ici
rien que pour souligner que la loi de Maxwell-Boltzmann décrit la
distribution des molécules sur leurs niveaux d'énergie quand elles
sont à l'èquilibre thermique à une température donnée.
Elle dépend explicitement de la température via le paramètre 
, et des autres variables thermodynamiques (V ou P, etc.)
indirectement via les niveaux d'énergie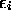 
.
Substituant eq.( 4.7) dans eq.(4.6), on obtient
où l'on a utilisé la relation entre l'énergie molaire moyenne (énergie interne molaire) et la fonction de répartition Q de l'équation (1.22), Chapitre 1.
