Next: Exemples
Up: Éléments de mécanique
Previous: Propriétés de W(n)
Les considérations précédentes suggèrent que le mode de
répartition des molécules sur les niveaux d'énergie donnant lieu à
l'état macroscopique d'un système de 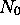 molécules (pour fixer les idées, on considérera toujours une mole de matière, c.à d.
molécules (pour fixer les idées, on considérera toujours une mole de matière, c.à d.  représentera toujours le nombre
d'Avogadro), à une température fixée, peut être obtenu en optimisant
W, ou
représentera toujours le nombre
d'Avogadro), à une température fixée, peut être obtenu en optimisant
W, ou 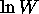 , par rapport aux différents
, par rapport aux différents  avec deux contraintes:
avec deux contraintes:
- Contrainte de conservation de masse: cette contrainte est d
écrite par eq.(1.11)
- Contrainte de conservation d'énergie (moyenne): On veut
obtenir une distribution correspondant à un état macroscopique d'
énergie moyenne (molaire) fixée, égale à
 . Les
. Les  doivent
donc respecter la condition
doivent
donc respecter la condition

Il est bien connu que l'optimization de  avec les
deux contraintes, eq.(1.11) et eq.(1.15), est
équivalente à l'optimization (sans contrainte) de la fonction auxiliaire
suivante
avec les
deux contraintes, eq.(1.11) et eq.(1.15), est
équivalente à l'optimization (sans contrainte) de la fonction auxiliaire
suivante

non seulement par rapport aux  , mais aussi par rapport aux
multiplicateurs de Lagrange
, mais aussi par rapport aux
multiplicateurs de Lagrange 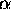 et
et  . L'optimization de G par
rapport à
. L'optimization de G par
rapport à 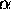 et
et  redonne précisément eq.(1.11) et eq.(1.15), respectivement. Par contre, avec
la relation de Stirling,
redonne précisément eq.(1.11) et eq.(1.15), respectivement. Par contre, avec
la relation de Stirling,
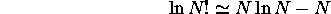
applicable pour N grand, on a
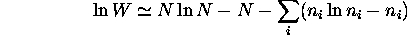
et l'optimization de G par rapport aux 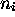
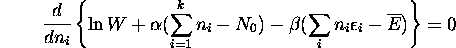
donne la

Notes:
- Dans le cas d'une énergie
 non-quantifiée
(continue), la loi de Maxwell-Boltzmann
non-quantifiée
(continue), la loi de Maxwell-Boltzmann
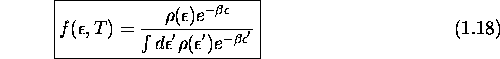
donne la densité de probabilité de trouver une molécule avec une
énergie égale à  ; la quantité
; la quantité 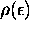 que l'on y trouve est la densité d'états d'énergie
que l'on y trouve est la densité d'états d'énergie  .
.
- Pour des mouvements composés mais séparables, l'énergie
de mouvement est la somme des énergies de mouvements séparés,


et la probabilité conjointe 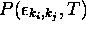 est
le produit des probabilités individuelles
est
le produit des probabilités individuelles  ,
, 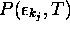






Next: Exemples
Up: Éléments de mécanique
Previous: Propriétés de W(n)
Cours WWW Cinetique Chimique
Wed Jan 8 16:28:09 EST 2003
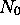 molécules (pour fixer les idées, on considérera toujours une mole de matière, c.à d.
molécules (pour fixer les idées, on considérera toujours une mole de matière, c.à d.  représentera toujours le nombre
d'Avogadro), à une température fixée, peut être obtenu en optimisant
W, ou
représentera toujours le nombre
d'Avogadro), à une température fixée, peut être obtenu en optimisant
W, ou 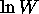 , par rapport aux différents
, par rapport aux différents  avec deux contraintes:
avec deux contraintes:
 . Les
. Les  doivent
donc respecter la condition
doivent
donc respecter la condition

 avec les
deux contraintes, eq.(
avec les
deux contraintes, eq.(
 , mais aussi par rapport aux
multiplicateurs de Lagrange
, mais aussi par rapport aux
multiplicateurs de Lagrange 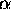 et
et  . L'optimization de G par
rapport à
. L'optimization de G par
rapport à 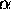 et
et  redonne précisément eq.(
redonne précisément eq.(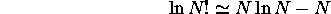
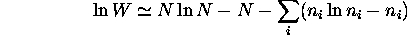
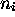
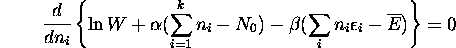

 non-quantifiée
(continue), la loi de Maxwell-Boltzmann
non-quantifiée
(continue), la loi de Maxwell-Boltzmann
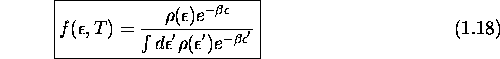
 ; la quantité
; la quantité 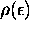 que l'on y trouve est la densité d'états d'énergie
que l'on y trouve est la densité d'états d'énergie  .
.


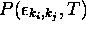 est
le produit des probabilités individuelles
est
le produit des probabilités individuelles  ,
,