Les deux panneaux (a) et (b) de la figure 1.6 illustrent la
distribution de Maxwell-Boltzmann pour l'occupation des niveaux
vibrationnels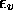 
, v=0-5, pour la molécule de 
, 
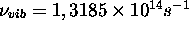(ou 
), à 
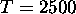et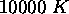 
, et pour la molécule NO, 
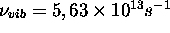, à T=1000 et 
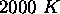. On voit que, géné
ralement, l'excitation vibrationnelle est faible aux températures
proches de la température ambiante.
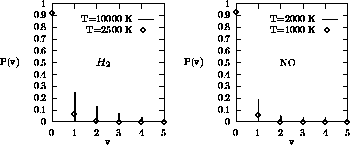
Figure: Distribution de Maxwell-Boltzmann sur les niveaux vibrationnels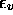 
, v=0-5, (a) de la molécule de 
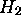, à T = 2500 et 
, (b) de la molécule de NO, à T = 1000 et 
.
La figure 1.7 illustre la distribution de molécules HCl sur
les niveaux rotationnels 
, à T=100 et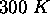 
. Pour
cette molécule, la séparation typique entre deux niveaux
rotationnels étant de l'ordre de 
, soit à peu près
de l'énergie thermique 
à 
, on trouve un degré d'excitation appréciable des rotations
à des températures proches de la température ambiante. Même
à plus basse température,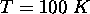 
, ce degré d'excitation est d
éjà fort appréciable. Notons l'existence d'un maximum dans la
distribution de Maxwell-Boltzmann sur les niveaux rotationnels, ce qui est
en net contraste avec les distributions sur des niveaux vibrationnels de la
figure 1.6. Ceci est du au fait que la dégéné
rescence des niveaux rotationnels augmentent avec J selon 
,
donnant à la distribution de Maxwell-Boltzmann l'accroissement initial
que l'on peut voir clairement à des J faibles sur les graphes de la
figure 1.7. À des J plus élevés, la décroissance
exponentielle caractéristique de la loi de Maxwell-Boltzmann l'emporte
sur l'accroissement du facteur dégénérescence, et la population d
écroit.
Figure 1.7: Distribution de Maxwell-Boltzmann sur les niveaux rotationnels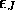 
, de la molécule de HCl, à T = 100 et 
.
Finalement, la figure 1.8 illustre la distribution de
Maxwell-Boltzmann pour le mouvement de translation pure, dont l'énergie
est non-quantifiée. La distribution pour ce genre de mouvement dans une
direction quelconque (x) est présenté au panneau (a) de la figure
1.8 sous forme d'une distribution (gaussienne) de la vitesse, 
. La masse d'inertie utilisée est celle de la molécule de HCl (
), et la distribution est présentée pour deux tempé
ratures, T=300 et 
. Il est parfois utile, dans le cas
tridimensionnel, d'introduire une distribution dite radiale,
obtenue en moyennant la distribution tridimensionnelle (isotrope) sur les
orientations du vecteur vitesse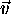 
. Pour la même molécule et
les mêmes températures, on montre au panneau (b) de la figure 1.8 la distribution radiale de la vitesse de translation de la molé
cule de HCl.
Figure: Distribution de Maxwell-Boltzmann (a) de la vitesse de translation 
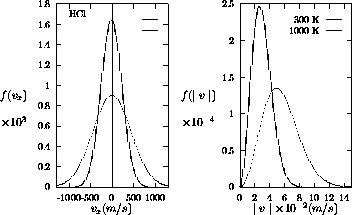
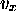pour la molécule de HCl, à T = 300 et 
, (b) de la vitesse tridimensionnelle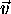 
, moyennée sur les orientations de 
(distribution radiale).