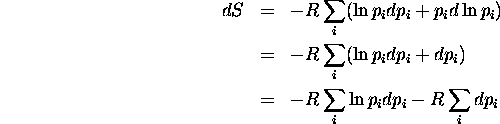
Pour établir cette équivalence, prenons la différentielle de eq.( 4.6):
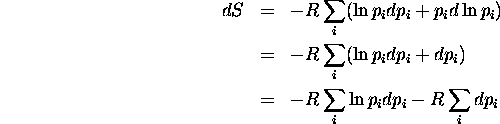
Or  , car la somme des probabilités devrait toujours
être égale à 1. Donc
, car la somme des probabilités devrait toujours
être égale à 1. Donc
Comme les 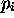 sont données par eq.(4.7
) , on a
sont données par eq.(4.7
) , on a
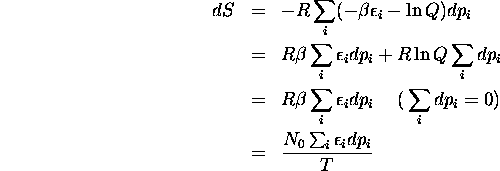
On a vu, au chapitre précédent, que 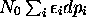 ne représente rien d'autre que la chaleur impliquée
dans le processus infinitésimal et réversible qui cause les
variations de populations
ne représente rien d'autre que la chaleur impliquée
dans le processus infinitésimal et réversible qui cause les
variations de populations 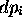 , c.à. d.
, c.à. d. 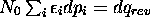 , et l'on réobtient, en effet, la définition
thermodynamique de l'entropie, eq.(4.2).
, et l'on réobtient, en effet, la définition
thermodynamique de l'entropie, eq.(4.2).