



Next: Point de vue
Up: Seconde loi
Previous: Énoncé
Du point de vue de la mécanique statistique, le second principe n'est
rien d'autre qu'une question de probabilité. On a vu, en effet, au
Chapitre 1, que plus le nombre de complexions 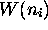 associé à
un état macroscopique est grand, plus cet état est probable, ou plus
facile à réaliser. En vertu de la définition statistique de S,
eq.(4.4), dire que l'entropie S d'un
système isolé augmente dans un processus (changement d'état)
spontané, c'est simplement reconnaitre que l'état macroscopique pour
lequel
associé à
un état macroscopique est grand, plus cet état est probable, ou plus
facile à réaliser. En vertu de la définition statistique de S,
eq.(4.4), dire que l'entropie S d'un
système isolé augmente dans un processus (changement d'état)
spontané, c'est simplement reconnaitre que l'état macroscopique pour
lequel 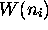 est plus grand est l'état le plus probable. Notons que
les deux états (initial et final) impliqués dans ce processus
peuvent différer non seulement par le schéma d'occupation des
niveaux d'énergie, réflétant une différence de
température, cf. eq.(4.7), mais aussi par
la disposition même des niveaux d'énergie, c.à d. par l'aspect
du spectre de niveaux d'énergie qui peut changer quand le volume change
par exemple.
est plus grand est l'état le plus probable. Notons que
les deux états (initial et final) impliqués dans ce processus
peuvent différer non seulement par le schéma d'occupation des
niveaux d'énergie, réflétant une différence de
température, cf. eq.(4.7), mais aussi par
la disposition même des niveaux d'énergie, c.à d. par l'aspect
du spectre de niveaux d'énergie qui peut changer quand le volume change
par exemple.
La définition statistique de l'entropie fait le mieux ressortir la
notion de désordre comme principe gouvernant les transformations
spontanées. Directement, 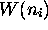 , donc
, donc  , mesure ce
désordre dans le schéma d'occupation des niveaux d'énergie.
Comme ces niveaux sont associés aux mouvements moléculaires
quantifiés, S mesure aussi indirectement le désordre au niveau de
ces mouvements. On peut donc faire usage de l'analyse du caractère plus
ou moins ordonné des mouvements moléculaires pour prédire ou
comprendre le sens d'une transformation donnée, une réaction
chimique par exemple.
, mesure ce
désordre dans le schéma d'occupation des niveaux d'énergie.
Comme ces niveaux sont associés aux mouvements moléculaires
quantifiés, S mesure aussi indirectement le désordre au niveau de
ces mouvements. On peut donc faire usage de l'analyse du caractère plus
ou moins ordonné des mouvements moléculaires pour prédire ou
comprendre le sens d'une transformation donnée, une réaction
chimique par exemple.
Cours WWW Cinetique Chimique
Wed Jan 8 16:28:09 EST 2003
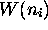 associé à
un état macroscopique est grand, plus cet état est probable, ou plus
facile à réaliser. En vertu de la définition statistique de S,
eq.(4.4), dire que l'entropie S d'un
système isolé augmente dans un processus (changement d'état)
spontané, c'est simplement reconnaitre que l'état macroscopique pour
lequel
associé à
un état macroscopique est grand, plus cet état est probable, ou plus
facile à réaliser. En vertu de la définition statistique de S,
eq.(4.4), dire que l'entropie S d'un
système isolé augmente dans un processus (changement d'état)
spontané, c'est simplement reconnaitre que l'état macroscopique pour
lequel 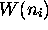 est plus grand est l'état le plus probable. Notons que
les deux états (initial et final) impliqués dans ce processus
peuvent différer non seulement par le schéma d'occupation des
niveaux d'énergie, réflétant une différence de
température, cf. eq.(4.7), mais aussi par
la disposition même des niveaux d'énergie, c.à d. par l'aspect
du spectre de niveaux d'énergie qui peut changer quand le volume change
par exemple.
est plus grand est l'état le plus probable. Notons que
les deux états (initial et final) impliqués dans ce processus
peuvent différer non seulement par le schéma d'occupation des
niveaux d'énergie, réflétant une différence de
température, cf. eq.(4.7), mais aussi par
la disposition même des niveaux d'énergie, c.à d. par l'aspect
du spectre de niveaux d'énergie qui peut changer quand le volume change
par exemple.
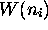 , donc
, donc  , mesure ce
désordre dans le schéma d'occupation des niveaux d'énergie.
Comme ces niveaux sont associés aux mouvements moléculaires
quantifiés, S mesure aussi indirectement le désordre au niveau de
ces mouvements. On peut donc faire usage de l'analyse du caractère plus
ou moins ordonné des mouvements moléculaires pour prédire ou
comprendre le sens d'une transformation donnée, une réaction
chimique par exemple.
, mesure ce
désordre dans le schéma d'occupation des niveaux d'énergie.
Comme ces niveaux sont associés aux mouvements moléculaires
quantifiés, S mesure aussi indirectement le désordre au niveau de
ces mouvements. On peut donc faire usage de l'analyse du caractère plus
ou moins ordonné des mouvements moléculaires pour prédire ou
comprendre le sens d'une transformation donnée, une réaction
chimique par exemple.