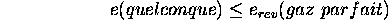
On va d'abord montrer que l'efficacité d'un cycle de Carnot quelconque ne peut jamais être supérieure à celle d'un cycle de Carnot réversible de gaz parfait opérant entre les deux mêmes températures
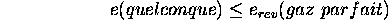
Pour ce faire, il suffit d'imaginer le supersystème suivant, composé
de la machine à tester et une machine réversible à gaz parfait
fonctionnant dans le sens inverse, les 2 machines partageant les mêmes
réservoirs thermiques à 
et 
, tel que la chaleur fournie par le gaz parfait lors de sa compression réversible à 
est intégralement utilisée par la machine à tester dans le processus isotherme correspondant. L'ensemble est supposé bien
isolé thermiquement du reste de l'univers.
Écrivons le bilan énergétique pour ce supersystème (les quantités primées appartiennent à la machine à tester):
On aura donc
Supposons maintenant que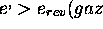 
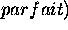. Comme 
est
positive, on aurait alors 
, et
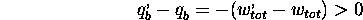
Ceci implique que de la chaleur nette 
reçue du
réservoir unique à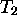 
aurait pû être convertie en
travail utile 
, en contradiction avec le principe
de Kelvin.
Par conséquent, l'énoncé de Kelvin équivaut à affirmer que
pour tout cycle de Carnot (machine de Carnot quelconque). Si cette machine est réversible, on peut faire tourner le tout en sens inverse; on trouve alors
Rassemblant les eqs.(4.29), (4.30), (4.14) et (4.16), on a encore une fois:
pour tout cycle de Carnot réversible, et
pour tout cycle de Carnot (réversible ou pas).
