Finalement, un processus cyclique quelconque peut toujours se décomposer en cycles de Carnot infinitésimaux adjacents, sur chacun desquels l'analyse précédent s'applique. Ceci implique que l'on peut généraliser les conclusions importantes que l'on y a trouvées pour les faire porter sur tout processus cyclique. On a, en particulier,
et l'inégalité de Clausius
De ces deux relations, eq.(4.33) ne fait que confirmer S dans son rôle de fonction d'état (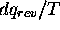
est une différentielle exacte), tandis que eq.(4.34) est déjà une expression de la seconde loi.
Pour s'en rendre compte, considérons maintenant une transformation quelconque 
.
En complétant ceci par le processus inverse réversible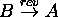 
, on peut
construire le cycle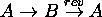 
auquel
l'application de l'inégalité de Clausius donne
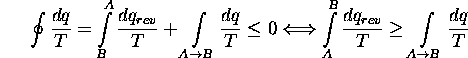
ou encore
Pour une transformation infinitésimale
et pour un système isolé:
On peut reconnaitre en eq.(4.35), la seconde loi énoncée en eq.(4.11) en identifiant la variation 
de l'entropie de l'environnement avec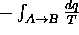 
,
ce qui équivaut à reconnaitre que, du point de vue de l'environnement infini du système, tout changement d'état du systéme est un processus réversible.
