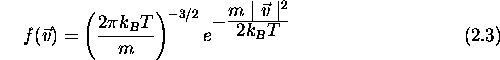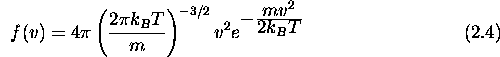Rappellant les résultats du chapitre précédent, eqs.(1.18), (1.33), (1.36), on peut tout d'abord ré-écrire la distribution de Maxwell-Boltzmann pour les translations sous la forme de diverses distributions de vitesse. On obtient notamment
, 
on note que cette distribution est isotrope: elle ne dépend que de la longueur v du vecteur vitesse 
, et non de son orientation. Il est utile pour cette raison d'introduire une distribution radiale: elle s'obtient en intégrant sur toutes les orientations possibles de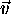 
(voir figure 1.8 du chapitre précédent).
L'intégration sur les angles dans la représentation polaire de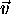 
, 
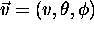donne un facteur 
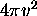. Il représente la surface de la coque sphérique de rayon v. La fonction 
représente
la densité de probabilité de trouver une molécule avec une vitesse de grandeur v, quelle que soit son orientation.
