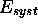Travail et chaleur

Selon la première loi, eq.(3.1), toute variation de l'énergie du système 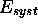est compensée par une variation correspondante (et de signe contraire) de l'énergie de l'environnement, c.à d.

pour un changement d'état infinitésimal, ou

pour un processus fini. La variation de l'énergie ne dépend que de l'état initial et de l'état final mais peut généralement se décomposer en plusieurs contributions dont la nature dépend du chemin suivi. On distingue deux types de contributions à 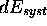(ou ):

1. Le travail: Il dénote une variation d'énergie accompagnant un déplacement ordonné, d'objets comme des molécules (travail de changement de volume), des électrons (travail électrique), une interface, etc., sous l'influence d'une force externe.
   • Un travail se définit donc généralement par

      

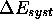     pour un déplacement infinitésimal, et

      

     pour un déplacement fini. Dans cette définition, le signe (+) assure que si les 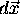(c.à d. les déplacements dans le système) sont orientés dans le même sens que la force alors le travail est compté positivement,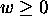, correspondant à une énergie fournie au (gagnée par le) système. Dans le cas contraire où les déplacements se font contre la force externe , le travail ainsi défini sera négatif dénotant une perte d'énergie du systè me qui ``effectue'' ce travail.

     Le travail que l'on rencontre le plus souvent en thermodynamique est le travail de changement de volume

      

     pour un changement de volume infinitésimal,

      

     pour un changement de volume fini

     Le travail est une fonction de passage. Il dépend du chemin suivi lors d'un changement d'état. Les exemples suivants illustrent ce point.

   • Exemples:

     On considère le passage, à tempé rature T constante, d'un gaz parfait d'un volume initial à un volume final 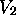, dans des conditions variées:

     1. Détente isotherme dans le vide:

         

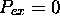
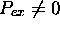     2. Détente (ou compression) isotherme contre une pression constante:

         

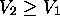        On vérifie que si (détente), et 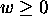si 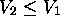(compression).

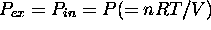     3. Détente (ou compression) isotherme réversible, tout au long du processus:

         

        On vérifie ici aussi que 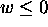si (détente), et 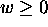si (compression). On note aussi que le travail fourni dans le cas d'une détente réversible 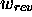est toujours supérieur à celui d'une détente irréversible, figure 3.2.

     
   Figure: Travail accompagnant une détente de gaz parfait. Notez que 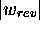est nécessairement plus grand que .
   

2. La chaleur: Toute variation de l'énergie interne qui n'est pas un travail, donc résultant d'excitations de mouvements aléatoires, est appelée chaleur. La chaleur peut donc s'identifier généralement avec la variation d'énergie interne dans tout processus à volume constant

    

   

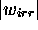   On peut définir aussi la chaleur comme cette variation d'énergie interne qui est associée à une variation de température à volume constant. On peut alors écrire

   

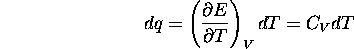
   où 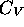est la capacité calorifique à volume constant définie au chapitre précédent.

   Selon ces définitions, il est clair que la chaleur est aussi une fonction de passage: elle dépend du chemin suivi au cours d'un changement d'état, puisqu'elle n'est identifiable avec une variation d'énergie interne que pour des processus à volume constant. Ceci ne signifie pas que l'on ne peut parler de chaleur que dans ces cas. Au contraire, dans tous les cas, la variation de l'énergie interne peut toujours se décomposer en la somme d'une contribution sous forme ``travail'' et d'une autre sous forme ``chaleur''

   

    

   avec réduction à

    

   seulement pour un processus à volume constant pour lequel le travail (mécanique, travail de changement de volume) est assurément nul.

   Remarques:

   1. On considère parfois eq.(3.15) comme l'expression de la première loi. Elle en est une en effet, dans la mesure où travail et chaleur dénotent des quantités d'énergie échangées entre le système et son environnement, et vues du point de vue du système.

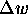   2. Question de notations: remarquez que l'on écrit w et q, au lieu de et 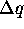respectivement, pour désigner un travail et une chaleur accompagnant un changement d'état fini. Ceci pour souligner que travail et chaleur sont des fonctions de passage, dont la grandeur dépend du chemin suivi. On réserve la notation 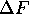pour désigner la variation finie d'une fonction d'état F, c.à d. pour signifier 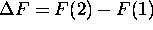. Dans la version infinitésimale, dans dq et dw ne désigne pas une différentielle comme d'habitude, mais simplement une quantité infinitésimale. On dit parfois que ce sont des ``différentielles inexactes''. Certains textes soulignent ceci en ajoutant une barre au d.

   3. Convention de signe: Toute variation d'énergie, travail ou chaleur, est comptée positive si elle représente un apport d'énergie au système, et négative dans le cas contraire, c.à d. si elle représente une perte d'énergie, du point de vue du système.

   Exemples

   À titre d'exemples, revenons aux trois processus de détente ou de compression isotherme d'un gaz parfait considérés ci-haut, et calculons la chaleur impliquée dans chacun de ces trois cas. Pour ce faire, rappelons que, pour un gaz parfait, l'énergie interne ne dépend que de la température T. Dans un processus isotherme, T est fixée, donc

   

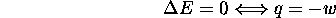
   dans ces trois cas. On a donc:

   1. Détente isotherme dans le vide:

       

   2. Détente (ou compression) isotherme contre une pression constante:

       

   3. Détente (ou compression) isotherme réversible:

       

Détente adiabatique réversible d'un gaz parfait monoatomique

Pour illustrer les concepts de travail et de chaleur dans l'application de la première loi, considérons le processus de détente adiabatique réversible

d'un gaz parfait monoatomique. On s'attend à ce que , puisque le système effectue du travail sans gain de chaleur de la part de l'environnement. Il sent donc une perte nette de l'énergie. Vérifions ceci.

Écrivons d'abord, pour une variation infinitésimale d'état le long du chemin adiabatique

puisque l'énergie d'un gaz parfait ne dépend que de T. En fait, comme le gaz est monoatomique, on peut même écrire [, voir eq.(1.38) du chapitre 1]

D'autre part, comme ce processus est adiabatique , de sorte que

Combinant eq.(3.21) et eq.(3.22), on obtient

d'où l'on tire, par intégration

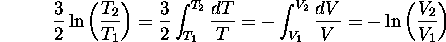
donc

Comme dans une détente, on conclut que

  
Figure 3.3: Différence entre une détente isotherme et une détente adiabatique de gaz parfait. Partant d'un même état initial, la détente adiabatique mène le système à un état final de plus basse température que le processus isotherme.