Rappelons ici l'expression de l'énergie interne molaire selon la mécanique statistique, (l'énergie moyenne molaire du chapitre 1):
Dans cette expression, 
est la probabité de trouver une molécule sur le niveau d'énergie 
, ou encore la population de ce niveau. Elle est décrite par la loi de Maxwell-Boltzmann, eq.(1.17) du Chapitre 1.
Toute variation de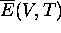 
ne peut provenir que soit d'une variation de la distribution 
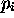des molécules sur les niveaux d'énergie 
fixes, variation qui est nécessairement associée à un changement de température à V constant et représente donc une chaleur, ou d'une variation des niveaux d'énergie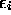 
eux-même, ce qui ne peut être induite que par un changement de volume à T constante, et représente un travail, figure 3.4. Mathématiquement, tout ceci se traduit par
avec, à la dernière ligne,l'identification évidente
L'indice rev affectant ces deux quantités est requise pour traduire le fait que les populations 
multipliant les variations infinitésimales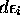 
dans eq.(3.44) demeurent inchangées. Chaleur et travail ont donc une expression statistique claire qui est en accord avec leur définition `thermodynamique' originale. De plus,
eq.(3.47) suggère l'identification suivante:
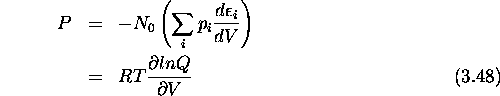
En particulier, pour un gaz parfait, comme Q ne dépend du volume V qu'à travers la contribution translationnelle 
, qui est proportionnelle à V selon eq.(1.36) du chapitre 1, on a
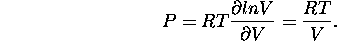
Figure 3.4: Différence entre chaleur et travail vue du point de vue de la mécanique statistique.
